Two-by-two ANOVA: Power simulation of the interaction test

Last modified: 2026-01-09

Application context

Effect of fertilizers

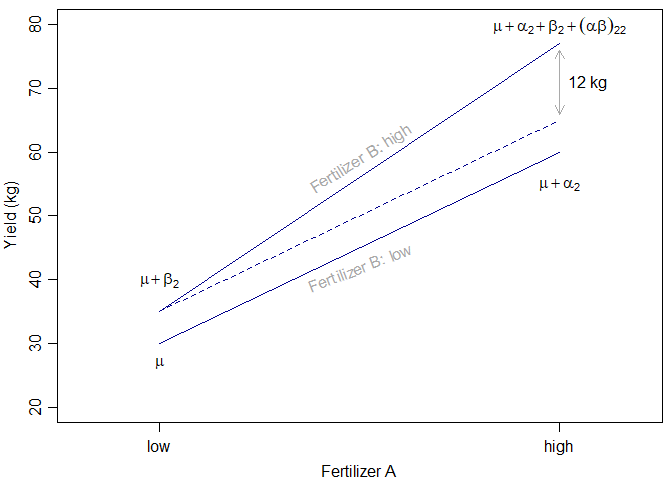
In an experiment, two fertilizers (A and B, each either low or high dose) will be combined and the yield of peas (Y) in kg be observed. Goal is to detect an increase of the Fertilizer-A effect by an additional 12 kg when combined with a high dose of Fertilizer B (interaction effect).

Model

Assumptions

Y_{ijk} = \mu + \alpha_i + \beta_j + (\alpha\beta)_{ij} + \varepsilon_{ijk}
\varepsilon_{ijk} \sim N(0, \sigma^2) \text{ i.i.d.}
i = 1, \dots, I; j = 1, \dots, J; k = 1, \dots, K
\alpha_1 = \beta_1 := 0

Hypothesis

H$0^{AB}\colon~ (\alpha\beta){ij} = 0 \text{ for all } i,j$

Setup

set.seed(1704)
n <- 96
dat <- data.frame(
  A = factor(rep(1:2, each = n/2), labels = c("low", "high")),
  B = factor(rep(rep(1:2, each = n/4), 2), labels = c("low", "high"))
)
X <- model.matrix(~ A*B, dat)
unique(X)

##    (Intercept) Ahigh Bhigh Ahigh:Bhigh
## 1            1     0     0           0
## 25           1     0     1           0
## 49           1     1     0           0
## 73           1     1     1           1

beta <- c(mu = 30, a2 = 30, b2 = 5, ab22 = 12)
means <- X %*% beta

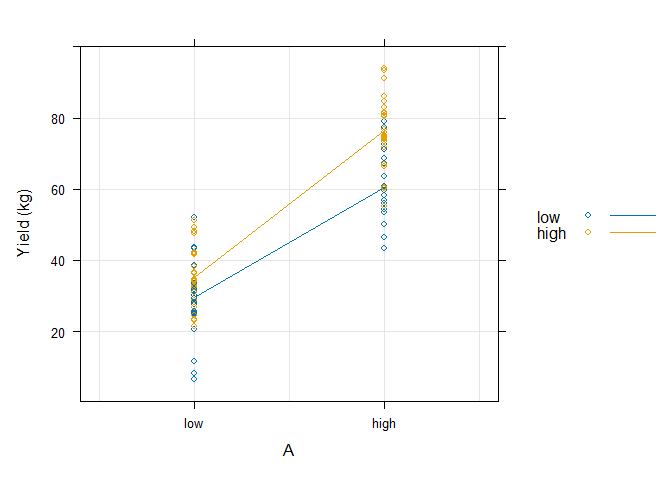
lattice::xyplot(I(means + rnorm(n, sd = 10)) ~ A, dat, groups = B,
                type = c("g", "p", "a"), auto.key = TRUE, ylab = "Yield (kg)")

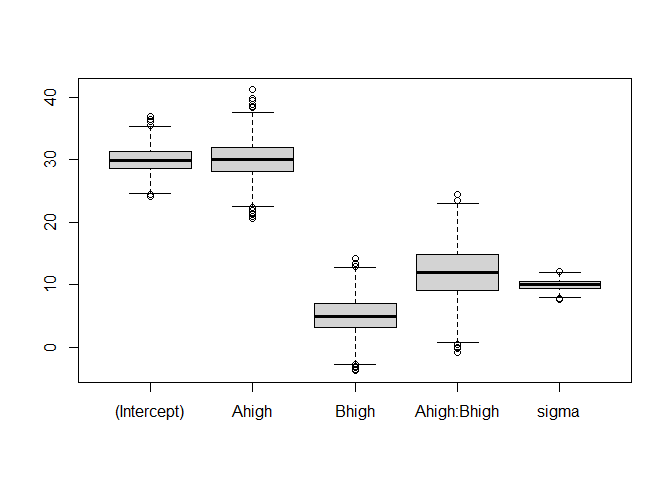
Parameter recovery

out <- replicate(2000, {
  y <- means + rnorm(n, sd = 10)   # y = mu + a + b + ab + e
  m <- aov(y ~ A * B, dat)
  c(coef(m), sigma = sigma(m))
})
boxplot(t(out))

Power simulation

pval <- replicate(2000, {
  y <- means + rnorm(n, sd = 10)
  m <- aov(y ~ A*B, dat)
  summary(m)[[1]]$"Pr(>F)"[3]      # test of interaction
})
mean(pval < 0.05)

## [1] 0.817

2.0 KiB Raw Blame History