lead_lmm/exercises/jsp.md

Exercise: Junior School Project

Load the Junior School Project collected from primary (U.S. term is elementary) schools in inner London in R. You might need to install the faraway package first with install.packages("faraway").

The data frame contains the following variables:

school	50 schools code 1–50
class	a factor with levels 1, 2, 3, and 4
gender	a factor with levels boy and girl
social	class of the father I = 1; II = 2; III nonmanual = 3; III manual = 4; IV = 5; V = 6; Long-term unemployed = 7; Not currently employed = 8; Father absent = 9
raven	test score
id	student id coded 1–1402
english	score on English
math	score on Maths
year	year of school

We want to investigate how math achievement is influenced by raven score and social class of the father. If you need a refresher on Raven’s Progressive Matrices, check here: https://en.wikipedia.org/wiki/Raven%27s_Progressive_Matrices. Basically, it is an intelligent test.

We will take a subset of the data, so that each student provides only one data point, for simplicity:

data("jsp", package = "faraway")
dat <- jsp |> subset(year == 0)

1. Create a new variable craven where raven is centered over all students

2. Create another variable gcraven where craven is centered over all schools. Create a variable mraven containing the centered average school means first, so that you can calculate

dat$gcraven <- dat$craven - dat$mraven

# Check your results
aggregate(craven ~ school, dat, mean) |> head()

##   school     craven
## 1      1 -2.6886533
## 2      2  0.1250722
## 3      3  2.0584055
## 4      4  0.9167389
## 5      5  2.3512627
## 6      6  0.4584055

aggregate(gcraven ~ school, dat, mean) |> head()

##   school       gcraven
## 1      1  1.253746e-15
## 2      2 -1.184075e-15
## 3      3 -1.421172e-15
## 4      4  1.184283e-15
## 5      5  5.075722e-16
## 6      6  0.000000e+00

3. Create a plot with lattice::xyplot() with gcraven on the x-axis and math on the y-axis and one panel for each school. Use type = c("p", "g", "r"). You can also use ggplot2 if you want to. What would be your conclusion about the need for school-specific slopes based on this plot?

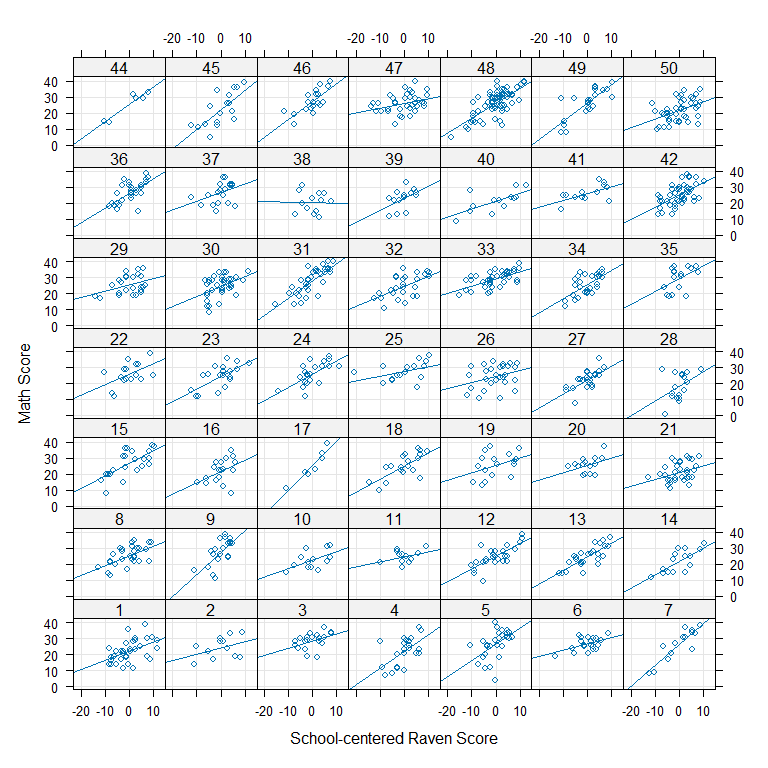
4. We will consider the following levels of the data:

   • Level 1: students
   • Level 2: schools

   And the variables associated with the levels:

   Level	Variable	Description
   2	school	50 schools code 1–50
   2	mraven	mean raven score of school (overall mean 0)
   1	social	class of the father (categorical)
   1	gcraven	centered test score (mean for each school 0)
   1	math	score on Maths

   Fit the following model containing school-specific intercepts and slopes with lme4::lmer()

   
   \begin{align*}
   \text{(Level 1)} \quad y_{ij} &= b_{0i} + b_{1i}\,gcraven_{ij} + b_{2i}\,social_{ij} + b_{3i}\,(gcraven_{ij}\times social_{ij}) + \varepsilon_{ij}\\
   \text{(Level 2)} \quad b_{0i} &= \beta_0 + \beta_4\,mraven_i + \upsilon_{0i} \\
                    \quad b_{1i} &= \beta_1 + \beta_5\,mraven_i + \upsilon_{1i}\\
                    \quad b_{2i} &= \beta_2\\
                    \quad b_{3i} &= \beta_3\\
   \text{(2) in (1)} \quad y_{ij} &= \beta_{0} + \beta_{1}\,gcraven_{ij} + \beta_{2}\,social_{ij} + \beta_{3}(gcraven_{ij}\times social_{ij})\\
                               &~~~ + \beta_{4}\,mraven_i + \beta_{5}\,(gcraven_{ij} \times mraven_{i})\\
                               &~~~ + \upsilon_{0i} + \upsilon_{1i}\,gcraven_{ij} + \varepsilon_{ij}
   \end{align*}
   

   with \boldsymbol\upsilon \sim N(\boldsymbol 0, \boldsymbol{\Sigma}_\upsilon) i.i.d., \varepsilon_{ij} \sim N(0, \sigma^2) i.i.d.

5. Interpret the parameters of the model:

   • How much does math score increases if the raven score for a student increases by one point for the reference social class of the father?
   • How much does math score increases when the raven score per school increases by one point for the reference social class of the father?
   • What is your conclusion about the interactions in the model. Are they needed?
   • Does the inclusion of social improve the model fit? How can we test this?